4 Standard results
In the sequel we determine all consistent Lagrangian interactions that can
be added to the free theory described by (1) and (4)-(7). This is done by means of solving the deformation equations (58)-(61), etc., with the help of specific cohomological
techniques. The interacting theory and its gauge structure are then deduced
from the analysis of the deformed solution to the master equation that is
consistent to all orders in the deformation parameter.
For obvious reasons, we consider only analytical, local, Lorentz covariant,
and Poincaré invariant deformations (i.e., we do not allow explicit
dependence on the spacetime coordinates). The analyticity of deformations
refers to the fact that the deformed solution to the master equation, (55), is analytical in the coupling constant  and reduces to
the original solution, (53), in the free limit
and reduces to
the original solution, (53), in the free limit
 . In
addition, we require that the overall interacting Lagrangian satisfies two
further restrictions related to the derivative order of its vertices:
. In
addition, we require that the overall interacting Lagrangian satisfies two
further restrictions related to the derivative order of its vertices:
- i)
- the maximum derivative order of each interaction vertex is equal
to two;
- ii)
- the differential order of each interacting field equation is
equal to that of the corresponding free equation (meaning that at most one
spacetime derivative can act on each field from the BF sector and at most
two spacetime derivatives on the tensor field
 ).
).
If we make the notation
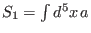 , with
, with  local, then
equation (58) (which controls the first-order deformation) takes
the local form
local, then
equation (58) (which controls the first-order deformation) takes
the local form
 |
(70) |
for some local  . It shows that the nonintegrated density of the
first-order deformation pertains to the local cohomology of
. It shows that the nonintegrated density of the
first-order deformation pertains to the local cohomology of  in ghost
number zero,
in ghost
number zero,
 , where
, where 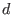 denotes the
exterior spacetime differential. The solution to (62) is unique up to
denotes the
exterior spacetime differential. The solution to (62) is unique up to
 -exact pieces plus divergences
-exact pieces plus divergences
 |
(71) |
If the general solution to (62) is trivial,
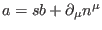 , then it can be made to vanish,
, then it can be made to vanish, 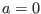 .
.
In order to analyze equation (62) we develop  according to the
antighost number
according to the
antighost number
 |
(72) |
and assume, without loss of generality, that the above decomposition stops
at some finite value of  . This can be shown for instance like in [43] (Section 3), under the sole assumption that the interacting
Lagrangian at order one in the coupling constant,
. This can be shown for instance like in [43] (Section 3), under the sole assumption that the interacting
Lagrangian at order one in the coupling constant, 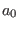 , has a finite, but
otherwise arbitrary derivative order. Inserting (64) into (62)
and projecting it on the various values of the antighost number, we obtain
the tower of equations (equivalent to (62))
, has a finite, but
otherwise arbitrary derivative order. Inserting (64) into (62)
and projecting it on the various values of the antighost number, we obtain
the tower of equations (equivalent to (62))
for some local
 . Equation (65) can always be replaced in strictly
positive values of the antighost number by
. Equation (65) can always be replaced in strictly
positive values of the antighost number by
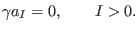 |
(76) |
Due to the second-order nilpotency of  (
(
 ), the
solution to (68) is unique up to
), the
solution to (68) is unique up to  -exact contributions
-exact contributions
 |
(77) |
If 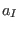 reduces only to
reduces only to  -exact terms,
-exact terms,
 , then
it can be made to vanish,
, then
it can be made to vanish,  . The nontriviality of the first-order
deformation
. The nontriviality of the first-order
deformation  is translated at its highest antighost number component into
the requirement that
is translated at its highest antighost number component into
the requirement that
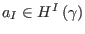 , where
, where
 denotes the cohomology of the exterior
longitudinal derivative
denotes the cohomology of the exterior
longitudinal derivative  in pure ghost number equal to
in pure ghost number equal to  . So, in
order to solve equation (62) (equivalent with (68) and (66)-(67)), we need to compute the cohomology of
. So, in
order to solve equation (62) (equivalent with (68) and (66)-(67)), we need to compute the cohomology of  ,
,
 , and, as it will be made clear below, also the
local homology of
, and, as it will be made clear below, also the
local homology of  ,
,
 .
.
From definitions (44)-(52) it is posible to show that
 is spanned by
is spanned by
 |
(78) |
the antifields
 , and all of their spacetime
derivatives as well as by the undifferentiated objects
, and all of their spacetime
derivatives as well as by the undifferentiated objects
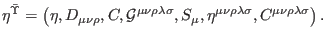 |
(79) |
In (70) and (71) we respectively used the notations
![$\displaystyle R_{\mu \nu \rho \vert\alpha \beta }=-\tfrac{1}{2}F_{\mu \nu \rho ...
...lpha ,\beta ]},\qquad D_{\mu \nu \rho }=\partial _{\lbrack \mu }A_{\nu \rho ]},$](img196.png) |
(80) |
with
 . It is useful to denote by
. It is useful to denote by
 and
and  the trace and respectively double trace
of
the trace and respectively double trace
of

 |
(81) |
The spacetime derivatives (of any order) of all the objects from (71) are removed from
 since they are
since they are  -exact. This can be seen directly from the last definition in (45),
the last present in (48), the first from (49), the second in
(50), the last from (51), and also using the relations
-exact. This can be seen directly from the last definition in (45),
the last present in (48), the first from (49), the second in
(50), the last from (51), and also using the relations
![$\displaystyle \partial _{\alpha }D_{\mu \nu \rho }=\gamma \left[ -\tfrac{1}{2}F...
...right) \right] \equiv \gamma \left[ \tfrac{1}{2}\mathcal{C}_{\mu \nu }\right] .$](img202.png) |
(82) |
Let
 be the elements with pure
ghost number
be the elements with pure
ghost number  of a basis in the space of polynomials in the objects (71). Then, the general solution to (68) takes the form (up, to
trivial,
of a basis in the space of polynomials in the objects (71). Then, the general solution to (68) takes the form (up, to
trivial,  -exact contributions)
-exact contributions)
![$\displaystyle a_{I}=\alpha _{I}\left( \left[ F_{\bar{A}}\right] ,\left[ \chi _{\Delta }^{\ast }\right] \right) e^{I}\left( \eta ^{\bar{\Upsilon}}\right) ,$](img205.png) |
(83) |
where
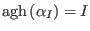 and
and
 . The notation
. The notation ![$ f([q])$](img208.png) means that
means that 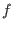 depends on
depends on  and
its spacetime derivatives up to a finite order. The objects
and
its spacetime derivatives up to a finite order. The objects
 (obviously nontrivial in
(obviously nontrivial in
 ) will be called
invariant `polynomials'. They are true polynomials with respect to all
variables (71) and their spacetime derivatives, excepting the
undifferentiated scalar field
) will be called
invariant `polynomials'. They are true polynomials with respect to all
variables (71) and their spacetime derivatives, excepting the
undifferentiated scalar field  , with respect to which
, with respect to which
 may be series. This is why we will keep the quotation marks around the word
polynomial(s). The result that we can replace equation (65) with the
less obvious one (68) for
may be series. This is why we will keep the quotation marks around the word
polynomial(s). The result that we can replace equation (65) with the
less obvious one (68) for  is a nice consequence of the fact
that the cohomology of the exterior spacetime differential is trivial in the
space of invariant `polynomials' in strictly positive antighost numbers.
These results on
is a nice consequence of the fact
that the cohomology of the exterior spacetime differential is trivial in the
space of invariant `polynomials' in strictly positive antighost numbers.
These results on
 can be synthesized in the
following array
can be synthesized in the
following array
 |
(84) |
where notations (2), (25)-(31), (32),
and (70) should be taken into account.
Inserting (75) in (66) we obtain that a necessary (but not
sufficient) condition for the existence of (nontrivial) solutions  is that the invariant `polynomials'
is that the invariant `polynomials'
 are (nontrivial) objects
from the local cohomology of Koszul-Tate differential
are (nontrivial) objects
from the local cohomology of Koszul-Tate differential
 in antighost number
in antighost number  and in pure ghost number zero,
and in pure ghost number zero,
 |
(85) |
We recall that
 is completely trivial in both
strictly positive antighost and pure ghost numbers (for instance,
see [42], Theorem 5.4, and [43]), so from now on it is
understood that by
is completely trivial in both
strictly positive antighost and pure ghost numbers (for instance,
see [42], Theorem 5.4, and [43]), so from now on it is
understood that by
 we mean the local cohomology
of
we mean the local cohomology
of  at pure ghost number zero. Using the fact that the free model
under study is a linear gauge theory of Cauchy order equal to five and the
general result from the literature [42,43] according to which the
local cohomology of the Koszul-Tate differential is trivial in antighost
numbers strictly greater than its Cauchy order, we can state that
at pure ghost number zero. Using the fact that the free model
under study is a linear gauge theory of Cauchy order equal to five and the
general result from the literature [42,43] according to which the
local cohomology of the Koszul-Tate differential is trivial in antighost
numbers strictly greater than its Cauchy order, we can state that
 |
(86) |
where
 represents the local cohomology of the
Koszul-Tate differential in antighost number
represents the local cohomology of the
Koszul-Tate differential in antighost number  . Moreover, it can be shown
that if the invariant `polynomial'
. Moreover, it can be shown
that if the invariant `polynomial'
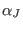 , with
, with
 , is trivial in
, is trivial in
 ,
then it can be taken to be trivial also in
,
then it can be taken to be trivial also in

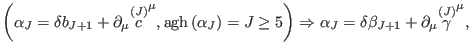 |
(87) |
with both
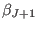 and
and
 invariant
`polynomials'. Here,
invariant
`polynomials'. Here,
 denotes
the invariant characteristic cohomology in antighost number
denotes
the invariant characteristic cohomology in antighost number  (the local
cohomology of the Koszul-Tate differential in the space of invariant
`polynomials'). An element of
(the local
cohomology of the Koszul-Tate differential in the space of invariant
`polynomials'). An element of
 is defined via an equation like (77), but with the
corresponding current an invariant `polynomial'. This result together with (
78) ensures that the entire invariant characteristic cohomology in
antighost numbers strictly greater than five is trivial
is defined via an equation like (77), but with the
corresponding current an invariant `polynomial'. This result together with (
78) ensures that the entire invariant characteristic cohomology in
antighost numbers strictly greater than five is trivial
 |
(88) |
It is possible to show that no nontrivial representative of
 or
or
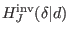 for
for  is allowed to
involve the spacetime derivatives of the fields [32] and [62]. Such a representative may depend at most on the undifferentiated
scalar field
is allowed to
involve the spacetime derivatives of the fields [32] and [62]. Such a representative may depend at most on the undifferentiated
scalar field  . With the help of relations (35)-(43
), it can be shown that
. With the help of relations (35)-(43
), it can be shown that
 and
and
 are spanned by the elements
are spanned by the elements
 |
(89) |
where
 |
(95) |
 |
(96) |
whit
 an arbitrary, smooth function depending
only on the undifferentiated scalar field
an arbitrary, smooth function depending
only on the undifferentiated scalar field  .
.
In contrast to the spaces
 and
and
 , which
are finite-dimensional, the cohomology
, which
are finite-dimensional, the cohomology
 (known to be
related to global symmetries and ordinary conservation laws) is
infinite-dimensional since the theory is free. Fortunately, it will not be
needed in the sequel.
(known to be
related to global symmetries and ordinary conservation laws) is
infinite-dimensional since the theory is free. Fortunately, it will not be
needed in the sequel.
The previous results on
 and
and
 in
strictly positive antighost numbers are important because they control the
obstructions to removing the antifields from the first-order deformation.
More precisely, we can successively eliminate all the pieces of antighost
number strictly greater that five from the nonintegrated density of the
first-order deformation by adding solely trivial terms, so we can take,
without loss of nontrivial objects, the condition
in
strictly positive antighost numbers are important because they control the
obstructions to removing the antifields from the first-order deformation.
More precisely, we can successively eliminate all the pieces of antighost
number strictly greater that five from the nonintegrated density of the
first-order deformation by adding solely trivial terms, so we can take,
without loss of nontrivial objects, the condition  into (64
). In addition, the last representative is of the form (75), where
the invariant `polynomial' is necessarily a nontrivial object from
into (64
). In addition, the last representative is of the form (75), where
the invariant `polynomial' is necessarily a nontrivial object from
 .
.
Ashkbiz Danehkar
2018-03-26
![]() and reduces to
the original solution, (53), in the free limit
and reduces to
the original solution, (53), in the free limit
![]() . In
addition, we require that the overall interacting Lagrangian satisfies two
further restrictions related to the derivative order of its vertices:
. In
addition, we require that the overall interacting Lagrangian satisfies two
further restrictions related to the derivative order of its vertices:
![]() , with
, with ![]() local, then
equation (58) (which controls the first-order deformation) takes
the local form
local, then
equation (58) (which controls the first-order deformation) takes
the local form
![]() according to the
antighost number
according to the
antighost number
 . Equation (65) can always be replaced in strictly
positive values of the antighost number by
. Equation (65) can always be replaced in strictly
positive values of the antighost number by
![]() is spanned by
is spanned by
![]() be the elements with pure
ghost number
be the elements with pure
ghost number ![]() of a basis in the space of polynomials in the objects (71). Then, the general solution to (68) takes the form (up, to
trivial,
of a basis in the space of polynomials in the objects (71). Then, the general solution to (68) takes the form (up, to
trivial, ![]() -exact contributions)
-exact contributions)
![]() is that the invariant `polynomials'
is that the invariant `polynomials'
![]() are (nontrivial) objects
from the local cohomology of Koszul-Tate differential
are (nontrivial) objects
from the local cohomology of Koszul-Tate differential
![]() in antighost number
in antighost number ![]() and in pure ghost number zero,
and in pure ghost number zero,
![]() or
or
![]() for
for ![]() is allowed to
involve the spacetime derivatives of the fields [32] and [62]. Such a representative may depend at most on the undifferentiated
scalar field
is allowed to
involve the spacetime derivatives of the fields [32] and [62]. Such a representative may depend at most on the undifferentiated
scalar field ![]() . With the help of relations (35)-(43
), it can be shown that
. With the help of relations (35)-(43
), it can be shown that
![]() and
and
![]() are spanned by the elements
are spanned by the elements
![]() and
and
![]() , which
are finite-dimensional, the cohomology
, which
are finite-dimensional, the cohomology
![]() (known to be
related to global symmetries and ordinary conservation laws) is
infinite-dimensional since the theory is free. Fortunately, it will not be
needed in the sequel.
(known to be
related to global symmetries and ordinary conservation laws) is
infinite-dimensional since the theory is free. Fortunately, it will not be
needed in the sequel.
![]() and
and
![]() in
strictly positive antighost numbers are important because they control the
obstructions to removing the antifields from the first-order deformation.
More precisely, we can successively eliminate all the pieces of antighost
number strictly greater that five from the nonintegrated density of the
first-order deformation by adding solely trivial terms, so we can take,
without loss of nontrivial objects, the condition
in
strictly positive antighost numbers are important because they control the
obstructions to removing the antifields from the first-order deformation.
More precisely, we can successively eliminate all the pieces of antighost
number strictly greater that five from the nonintegrated density of the
first-order deformation by adding solely trivial terms, so we can take,
without loss of nontrivial objects, the condition ![]() into (64
). In addition, the last representative is of the form (75), where
the invariant `polynomial' is necessarily a nontrivial object from
into (64
). In addition, the last representative is of the form (75), where
the invariant `polynomial' is necessarily a nontrivial object from
![]() .
.