8 Some solutions to the consistency equations
Equations (130)-(135) and (141)-(142),
required by the consistency of the first-order deformation, possess the
following classes of solutions, interesting from the point of view of
cross-couplings between the BF field sector and the tensor field with the
mixed symmetry  .
.
- I.
- The real constants
 and
and 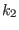 are arbitrary (
are arbitrary (
 ), functions
), functions  and
and 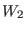 are some
arbitrary, real, smooth functions of the undifferentiated scalar field, and
are some
arbitrary, real, smooth functions of the undifferentiated scalar field, and
The above formulas allow one to infer directly the solution in the general
case  . This class of solutions can be equivalently reformulated as:
the real constants
. This class of solutions can be equivalently reformulated as:
the real constants  and
and 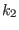 are arbitrary (
are arbitrary (
 ), functions
), functions  and
and  are some arbitrary, real, smooth
functions of the undifferentiated scalar field, and
are some arbitrary, real, smooth
functions of the undifferentiated scalar field, and
The last formulas are useful at writing down the solution in the particular
case  .
.
- II.
- The real constants
 and
and 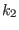 are arbitrary (
are arbitrary (
 ), functions
), functions  and
and  are some
arbitrary, real, smooth functions of the undifferentiated scalar field, and
are some
arbitrary, real, smooth functions of the undifferentiated scalar field, and
The above formulas allow one to infer directly the solution in the general
case  . This class of solutions can be equivalently reformulated as:
the real constants
. This class of solutions can be equivalently reformulated as:
the real constants  and
and 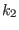 are arbitrary (
are arbitrary (
 ), functions
), functions  and
and  are some arbitrary, real, smooth
functions of the undifferentiated scalar field, and
are some arbitrary, real, smooth
functions of the undifferentiated scalar field, and
The last formulas are useful at writing down the solution in the particular
case  .
.
- III.
- The real constants
 and
and 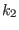 are arbitrary (
are arbitrary (
 ), functions
), functions  and
and  are some arbitrary,
real, smooth functions of the undifferentiated scalar field, and
are some arbitrary,
real, smooth functions of the undifferentiated scalar field, and
The above formulas allow one to infer directly the solution in the general
case  . This class of solutions can be equivalently reformulated as:
the real constants
. This class of solutions can be equivalently reformulated as:
the real constants  and
and 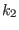 are arbitrary (
are arbitrary (
 ), functions
), functions  and
and  are some arbitrary, real, smooth functions
of the undifferentiated scalar field, and
are some arbitrary, real, smooth functions
of the undifferentiated scalar field, and
The last formulas are useful at writing down the solution in the particular
case  .
.
For all classes of solutions the emerging interacting theories display the
following common features:
- 1.
- there appear nontrivial cross-couplings between the BF fields and
the tensor field with the mixed symmetry
 ;
;
- 2.
- the gauge transformations are modified with respect to those of
the free theory and the gauge algebras become open (only close on-shell);
- 3.
- the first-order reducibility functions are changed during the
deformation process and the first-order reducibility relations take place
on-shell.
Nevertheless, there appear the following differences between the above classes
of solutions at the level of the higher-order reducibility:
- a)
- for class I the second-order reducibility functions are modified
with respect to the free ones and the corresponding reducibility relations
take place on-shell. The third-order reducibility functions remain those
from the free case and hence the associated reducibility relations hold
off-shell;
- b)
- for class II both the second- and third-order reducibility
functions remain those from the free case and hence the associated
reducibility relations hold off-shell;
- c)
- for class III all the second- and third-order reducibility
functions are deformed and the corresponding reducibility relations only
close on-shell.
Ashkbiz Danehkar
2018-03-26
![]() .
.