To provide equations governing relativistic dynamics of matter, we
use the Bianchi identities
![$\displaystyle \nabla_{\lbrack e}R_{ab]cd}=0.$](img85.png) |
(35) |
On substituting Eq. (29) into Eq. (35), we
get the dynamic formula for the Weyl conformal
curvature[3,40,41]:
![$\displaystyle \nabla^{d}C_{abcd}=-\nabla_{\lbrack a}(R_{b]c}-{\textstyle{\frac{...
...\lbrack a}(T_{b]c}-{\textstyle{\frac{1}{3}}}g_{b]c}T_{d} {}^{d})\equiv J_{abc}.$](img86.png) |
(36) |
On decomposing Eq. (36) along and orthogonal to a
4-velocity
vector, we obtain constraint (
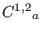 ) and propagation (
) and propagation (
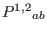 ) equations of the Weyl fields in a form analogous to the
Maxwell
equations[10,42,43,44]:
) equations of the Weyl fields in a form analogous to the
Maxwell
equations[10,42,43,44]:
The twice contracted Bianchi identities present the conservation of
the total energy momentum tensor, namely
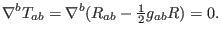 |
(41) |
It is split into a timelike and a spacelike momentum constraints:
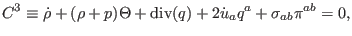 |
(42) |
They provide the conservation law of energy-momentum, i.
e., how matter determines the geometry, and describe the motion of
matter.
Ashkbiz Danehkar
2018-03-26