Next: 6 Soliton characteristics Up: Electron-acoustic solitary waves in Previous: 4 Nonlinear analysis for
We next investigate the conditions for existence of solitons. First, we need
to ensure that the origin at ![]() is a root and a local maximum of
is a root and a local maximum of ![]() in Eq. (33), i.e.,
in Eq. (33), i.e.,
![]() ,
,
![]() and
and
![]() at
at ![]() [43,44,45], where primes denote derivatives
with respect to
[43,44,45], where primes denote derivatives
with respect to ![]() . It is easily seen that the first two constraints are
satisfied. We thus impose the condition
. It is easily seen that the first two constraints are
satisfied. We thus impose the condition
An upper limit for ![]() is found through the fact that the cool electron
density becomes complex at
is found through the fact that the cool electron
density becomes complex at
![]() , and hence the largest soliton
amplitude satisfies
, and hence the largest soliton
amplitude satisfies
![]() . This yields
the following equation for the upper limit in M:
. This yields
the following equation for the upper limit in M:
For comparison, for a Maxwellian distribution (here recovered as
![]() ), the constraints reduce to
), the constraints reduce to
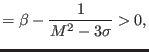 |
(37) | |
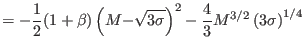 |
||
![$\displaystyle +\beta\left( 1-\exp\left[ -\tfrac{1}{2}\left( {M-}\sqrt{3{\sigma} }\right) ^{2}\right] \right)$](img195.png) |
||
| (38) |
In the opposite limit of ultrastrong suprathermality, i.e.,
![]() , the Mach number threshold approaches a non-zero limit
, the Mach number threshold approaches a non-zero limit
![]() , which is essentially the thermal speed, as noted
above (recall that
, which is essentially the thermal speed, as noted
above (recall that
![]() by assumption). The upper limit
by assumption). The upper limit
![]() is then given by
is then given by
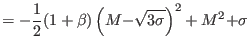 |
||
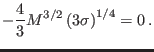 |
(39) |
We have studied the existence domain of electron-acoustic solitary waves for
different values of the parameters. The results are depicted in
Figs. 2-3.
Solitary structures of the electrostatic potential may occur in the range
![]() , which depends on the parameters
, which depends on the parameters ![]() ,
, ![]() , and
, and
![]() . We recall that we have also assumed that cool electrons are
supersonic (in the sense
. We recall that we have also assumed that cool electrons are
supersonic (in the sense
![]() )
[43,44,45], and the hot electrons subsonic
(
)
[43,44,45], and the hot electrons subsonic
(![]() ), and care must be taken not to go beyond the limits of the plasma
model.
), and care must be taken not to go beyond the limits of the plasma
model.
![\includegraphics[
height=3.4722in,
width=2.5573in
]{figures/fig5.eps}](img206.png)
|
The interval
![]() where solitons may exist is depicted in Fig.
2, in two opposite cases: in (a) and (c) two very low, and in (b) one
very high value of
where solitons may exist is depicted in Fig.
2, in two opposite cases: in (a) and (c) two very low, and in (b) one
very high value of ![]() . We thus see that for both a quasi-Maxwellian
distribution and one with a large excess suprathermal component of hot
electrons, both
. We thus see that for both a quasi-Maxwellian
distribution and one with a large excess suprathermal component of hot
electrons, both ![]() and
and ![]() decrease with an increase in the relative
density parameter
decrease with an increase in the relative
density parameter ![]() for fixed
for fixed ![]() and soliton speed
and soliton speed ![]() . Further,
the upper limit falls off more rapidly, and thus the existence domain in Mach
number becomes narrower for higher values of the hot-to-cool electron density
ratio. Comparing the two frames (a) and (b) in Fig. 2, we immediately
notice that suprathermality (low
. Further,
the upper limit falls off more rapidly, and thus the existence domain in Mach
number becomes narrower for higher values of the hot-to-cool electron density
ratio. Comparing the two frames (a) and (b) in Fig. 2, we immediately
notice that suprathermality (low ![]() ) results in solitons propagating at
lower Mach number values, a trend which is also seen in Fig. 2c.
Another trend that is visible in Figs. 2-3a is that
increased thermal pressure effects of the cool electrons, manifested through
increasing
) results in solitons propagating at
lower Mach number values, a trend which is also seen in Fig. 2c.
Another trend that is visible in Figs. 2-3a is that
increased thermal pressure effects of the cool electrons, manifested through
increasing ![]() , also lead to a narrowing of the Mach number range that
can support solitons. Finally, we note that for
, also lead to a narrowing of the Mach number range that
can support solitons. Finally, we note that for
![]() , the upper limit
found from Eq. (36) rises above the limit
, the upper limit
found from Eq. (36) rises above the limit ![]() required by the
assumptions of the model, and the latter then forms the upper limit.
required by the
assumptions of the model, and the latter then forms the upper limit.
Interestingly, in Figs. 2-3 the existence region appears to
shrink down to nil, as the curves approach each other for high ![]() values.
This is particularly visible in Fig. 2c, for a very low value of
values.
This is particularly visible in Fig. 2c, for a very low value of
![]() (
(
![]() ). This is not an unexpected result, as high values of
). This is not an unexpected result, as high values of
![]() are equivalent to a reduction in cool electron relative density, which
leads to our model breaking down if the inertial electrons vanish. We recall
that a value
are equivalent to a reduction in cool electron relative density, which
leads to our model breaking down if the inertial electrons vanish. We recall
that a value ![]() is a rather abstract case, as it corresponds to a
forbidden regime, since Landau damping will prevent electron-acoustic
oscillations from propagating. Similarly, a high value of the temperature
ratio, such as
is a rather abstract case, as it corresponds to a
forbidden regime, since Landau damping will prevent electron-acoustic
oscillations from propagating. Similarly, a high value of the temperature
ratio, such as
![]() , takes us outside the physically reasonable
domain. Nevertheless, as it appears that the lower and upper limits in
, takes us outside the physically reasonable
domain. Nevertheless, as it appears that the lower and upper limits in ![]() approach each other asymptotically for high values of
approach each other asymptotically for high values of ![]() , we have carried
out calculations for increasing
, we have carried
out calculations for increasing ![]() , up to
, up to ![]() for
for
![]() as
an academic exercise, and can confirm that the two limits do not actually
intersect.
as
an academic exercise, and can confirm that the two limits do not actually
intersect.
![\includegraphics[
height=5.7545in,
width=2.5097in
]{figures/fig6.eps}](img213.png)
|
Figure 3 shows the range of allowed Mach numbers as a function of
![]() , for various values of the temperature ratio
, for various values of the temperature ratio ![]() . As discussed
above, increasing
. As discussed
above, increasing ![]() towards a Maxwellian distribution (
towards a Maxwellian distribution (
![]() ) broadens the Mach number range and yields higher values of
Mach number. On the other hand, both upper and lower limits decrease as the
limiting value
) broadens the Mach number range and yields higher values of
Mach number. On the other hand, both upper and lower limits decrease as the
limiting value
![]() is approached. The qualitative conclusion is analogous
to the trend in Fig. 2: stronger excess suprathermality leads to
solitons occurring in narrower ranges of
is approached. The qualitative conclusion is analogous
to the trend in Fig. 2: stronger excess suprathermality leads to
solitons occurring in narrower ranges of ![]() . Furthermore, as illustrated in
Figs. 2 and 3a, the Mach number threshold
. Furthermore, as illustrated in
Figs. 2 and 3a, the Mach number threshold ![]() approaches
the upper limit
approaches
the upper limit ![]() for high values of
for high values of ![]() and
and ![]() : both
increased hot-electron density and cool-electron thermal effects shrink the
permitted soliton existence region.
: both
increased hot-electron density and cool-electron thermal effects shrink the
permitted soliton existence region.
Figure 3b depicts the range of allowed Mach numbers as a function of
![]() for various values of the density parameter
for various values of the density parameter ![]() (for a fixed
indicative
(for a fixed
indicative ![]() value). We note that both curves decrease with an increase
in
value). We note that both curves decrease with an increase
in ![]() . Although it lies in the damped region, we have also depicted a
high
. Although it lies in the damped region, we have also depicted a
high ![]() regime for comparison (solid-crosses curve).
regime for comparison (solid-crosses curve).
We conclude this section with a brief comparison of our work with that of Ref.
[39]. The latter did not consider existence domains at all,
let alone their dependence on plasma parameters, but merely plotted some
Sagdeev potentials and associated soliton potential profiles for chosen values
of some of the parameters, so as to extract some trends. En passant, there is
indirect mention of an upper limit in ![]() , in that it is commented that as
increasing values of
, in that it is commented that as
increasing values of ![]() are considered, at some stage solitary waves cease to
exist. [39]
are considered, at some stage solitary waves cease to
exist. [39]
![\includegraphics[
height=2.111in,
width=3.1384in
]{figures/fig8.eps}](img214.png)
|
![\includegraphics[
height=3.2534in,
width=2.5028in
]{figures/fig9.eps}](img215.png)
|
Ashkbiz Danehkar